Plotting

Summary

Plotting
Functions
Plot2D	Plots a system of 2 variables
PlotCurve3D	Plots a curve given by implicit equations in 3 variables.
Plot3D	Plots a system of 3 variables using maple internal plotting functions.
Plot3Dglsurf	Plots a system of 3 variables using glsurf.
Plot3Dsurfex	Plots a system of 3 variables using surfex (software based on surf).
PlotWorkspace	Plot the border of a manipulator workspace
Configurations	Computes the different possible positions.
PlotRobot2D	Plot a planar manipulator
PlotRobot3D	Plot a 3D manipulator
PlotCell3D	Plot the cells returned CellDecomposition or CellDecompositionPlus
PlotCell2D	Plot the cells returned CellDecomposition or CellDecompositionPlus
SetCellColors	Set colors to the numbers of solutions obtained by NumberOfSolutionsPlus
Path	Interpolate points linearly.
Trajectory	Display a given trajectory.
ImageTrajectory	Display a given trajectory.

Functions

Plot2D

Plot2D := proc (
    sys ::{algebraic, equation(algebraic), list({algebraic,equation(algebraic), algebraic<algebraic}), list(list({algebraic,equation(algebraic), algebraic<algebraic}))},
    e1 ::name = range,
    e2 ::name = range,
    {
    points ::truefalse := false,
    [ notest, draft ] ::truefalse := false
    }
)

Plots a system of 2 variables

Parameters

sys	a list or a list of list of polynomials: the system
v1 = r1	v1 is a name of sys and r1 a range of values
v2 = r2	v2 is a name of sys and r2 a range of values
points = bool (optional)	bool is a boolean: if false, isolated points are ignored; default value: false;
notest = b (optional)	b is a boolean; when b is true the inequality and real constraints are ignored; default value: true;
opts (optional)	arguments passed to the maple function plots:-implicitplot

Returns

A graphic: the solutions of the system.

when sys is a polynomial, the graphic is the zeroes of this polynomial
when sys is a list of polynomials [p1,...,pk], the graphic is the zeroes of the system p1=0 and ... and pk=0
when sys is a list of list of polynomials [L1,...,Lk], the graphic is the union of the zeroes of each system L1, ..., Lk.

PlotCurve3D

PlotCurve3D := proc (
    sys ::{algebraic, equation(algebraic), list({algebraic,equation(algebraic), algebraic<algebraic}), list(list({algebraic,equation(algebraic), algebraic<algebraic}))},
    ineq ::list({polynom, polynom<polynom}) := [],
    e1 ::name = range := sort ([op(indets([sys,x,y,z],name))])[1] =-5..5,
    e2 ::name = range := sort ([op(indets([sys,x,y,z],name) minus {lhs(e1)})])[1] =-5..5,
    e3 ::name = range := sort ([op(indets([sys,x,y,z],name) minus {lhs(e1),lhs(e2)})])[1] =-5..5,
    {
    grid ::integer := 30,
    output ::identical(list,display) := ':-display'
    }
)

Plots a curve given by implicit equations in 3 variables.

Parameters

sys	a list or a list of list of polynomials: the system
v1 = r1	v1 is a name of sys and r1 a range of values
v2 = r2	v2 is a name of sys and r2 a range of values
v3 = r3	v3 is a name of sys and r3 a range of values
grid = i (optional)	i is an integer, the number of samples points; default value: 20.
output = keyword (optional)	keyword is either list or display: display (resp. list) returns a graph (resp. a list).

Returns

A graphic: the solutions of the system.

when sys is a list of polynomials [p1,...,pk], the graphic is the zeroes of the system p1=0 and ... and pk=0
when sys is a list of list of polynomials [L1,...,Lk], the graphic is the union of the zeroes of each system L1, ..., Lk.

Example

> PlotCurve3D ([x^2+y^2-1, z^2-x],grid=100,title="cusp");

Plot3D

Plot3D := proc (
    sys ::{algebraic, equation(algebraic), list({algebraic,equation(algebraic), algebraic<algebraic}), list(list({algebraic,equation(algebraic), algebraic<algebraic}))},
    ineq ::list({polynom, polynom<polynom}) := [],
    e1 ::name = range := sort ([op(indets([sys,x,y,z],name))])[1] =-5..5,
    e2 ::name = range := sort ([op(indets([sys,x,y,z],name) minus {lhs(e1)})])[1] =-5..5,
    e3 ::name = range := sort ([op(indets([sys,x,y,z],name) minus {lhs(e1),lhs(e2)})])[1] =-5..5,
    {
    points ::truefalse := false,
    crossingrefine ::truefalse := false,
    grid ::integer := 10,
    border ::constant := 10^(-30),
    output ::identical(list,display) := ':-display',
    noverbose ::truefalse := false,
    verboserate ::integer := -10
    }
)

Plots a system of 3 variables using maple internal plotting functions.

Parameters

sys	a list or a list of list of polynomials: the system
v1 = r1	v1 is a name of sys and r1 a range of values
v2 = r2	v2 is a name of sys and r2 a range of values
v3 = r3	v3 is a name of sys and r3 a range of values
points = bool (optional)	bool is a boolean: if false, isolated points are ignored; default value: false;
grid = i (optional)	i is an integer leading to a grid size i x i; default value: 20.
border = e (optional)	e is a numeric value: defines the precision on the border; default value: 0.0001.
crossingrefine = bool (optional)	bool is a boolean: if true, the mesh follows the cross of the different surfaces; default value: false.
output = keyword (optional)	keyword is either list or display: display (resp. list) returns a graph (resp. a list).
noverbose = b (optional)	b is a boolean: if true, no verbose is displayed; default value: false
verboserate = i (optional)	i is an integer: if positive (resp. negative) the number (resp. the pourcentage) of cells computed before displaying a new verbose line; default value: -10

Returns

A graphic: the solutions of the system.

when sys is a polynomial, the graphic is the zeroes of this polynomial
when sys is a list of polynomials [p1,...,pk], the graphic is the zeroes of the system p1=0 and ... and pk=0
when sys is a list of list of polynomials [L1,...,Lk], the graphic is the union of the zeroes of each system L1, ..., Lk.

Plot3Dglsurf

Plot3Dglsurf := proc (
    sys ::{algebraic, equation(algebraic), list({algebraic,equation(algebraic)}), list(list({algebraic,equation(algebraic)}))},
    e1 ::name = range,
    e2 ::name = range,
    e3 ::name = range,
    {
    points ::truefalse := false,
    scale ::identical(constrained, unconstrained) := 'unconstrained'
    }
)

Plots a system of 3 variables using glsurf.

Parameters

sys	a list or a list of list of polynomials: the system
v1 = r1	v1 is a name of sys and r1 a range of values
v2 = r2	v2 is a name of sys and r2 a range of values
v3 = r3	v3 is a name of sys and r3 a range of values
points = bool (optional)	bool is a boolean: if false, isolated points are ignored; default value: false;
scaled = keyword (optional)	keyword is one of ‘constrained’ or ‘unconstrained’ for the scaling; default value: scaled = unconstrained.

Returns

A graphic: the solutions of the system.

when sys is a polynomial, the graphic is the zeroes of this polynomial
when sys is a list of polynomials [p1,...,pk], the graphic is the zeroes of the system p1=0 and ... and pk=0
when sys is a list of list of polynomials [L1,...,Lk], the graphic is the union of the zeroes of each system L1, ..., Lk.

Plot3Dsurfex

Plot3Dsurfex := proc (
    sys ::{algebraic, equation(algebraic), list({algebraic, equation(algebraic), algebraic<algebraic}), list(list({algebraic,equation(algebraic)}))},
    ineq ::list({polynom, polynom<polynom}) := [],
    e1 ::name = range := sort ([op(indets([sys,x,y,z]))])[1] =-1..1,
    e2 ::name = range := sort ([op(indets([sys,x,y,z]))])[2] =-1..1,
    e3 ::name = range := sort ([op(indets([sys,x,y,z]))])[3] =-1..1,
    {
    points ::truefalse := false,
    scale ::identical(constrained, unconstrained) := 'unconstrained'
    }
)

Plots a system of 3 variables using surfex (software based on surf).

Parameters

sys	a list or a list of list of polynomials and/or inequalities: the system
ineq (optional)	list of polynomials: extra positive inequalities; default value: []
v1 = r1 (optional)	v1 is a name of sys and r1 a range of values; default value: v1=-1..1 where v1 is a variable of sys
v2 = r2 (optional)	v2 is a name of sys and r2 a range of values default value: v2=-1..1 where v2 is a variable of sys
v3 = r3 (optional)	v3 is a name of sys and r3 a range of values default value: v3=-1..1 where v3 is a variable of sys
points = bool (optional)	bool is a boolean: if false, isolated points are ignored; default value: false;
scaled = keyword (optional)	keyword is one of ‘constrained’ or ‘unconstrained’ for the scaling; default value: scaled = unconstrained.

Returns

A graphic: the solutions of the system.

when sys is a polynomial, the graphic is the zeroes of this polynomial
when sys is a list of polynomials [p1,...,pk], the graphic is the zeroes of the system p1=0 and ... and pk=0
when sys is a list of list of polynomials [L1,...,Lk], the graphic is the union of the zeroes of each system L1, ..., Lk.

PlotWorkspace

PlotWorkspace := proc (
    robot ::Manipulator,
    spec ::seq(name=constant),
    disp ::seq(identical(type1,type2, constraints,infinite)) := ('type1','type2','constraints','infinite'),
    vars ::{list(name), identical(articular, pose)} := 'articular',
    ranges ::seq(name=range) := NULL,
    {
    notest ::truefalse := false
    }

)

Plot the border of a manipulator workspace

Parameters

robot	a object of type Manipulator
spec	sequence of name=constant: the specification of the known variables (the articular values or the pose values, or other)
disp (optional)	a sequence of keywords among type1, type2, constraints and infinite: selects the graphics to plot; default value: all the keywords
vars (optional)	the display variables, that can be referred as:

one of the keyword ‘articular’ or ‘pose’
a list of 2 variable names
the default value is ‘articular’
if ranges is provided, the variables superseed those of vars

ranges (optional)	a sequence of the form v1=n1..n2, v2=m1..m2 where v1, v2 are 2 variables and n1,n2,m1,m2 are numerical values; when ranges is not specified, the default range is taken from the field robot:-DefaultPlotRange if it exists, and is -5..5 otherwise.
notest = b (optional)	b is a boolean; when b is true the inequality and real constraints are ignored; default value: true;

Returns

A graphic containing:

The singularities of type 1
The singularities of type 2
The configurations with infinitely many solutions in all tha variables (including the passive variables)
The border induced by the constraints

Example

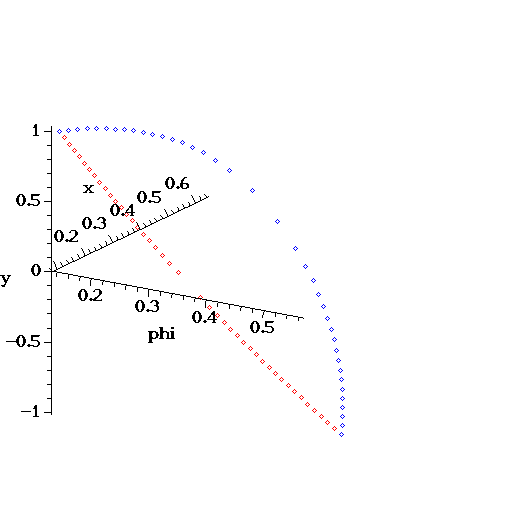
> rprrp := Parallel_RPRRP ():
> PlotWorkspace (rprrp, articular);

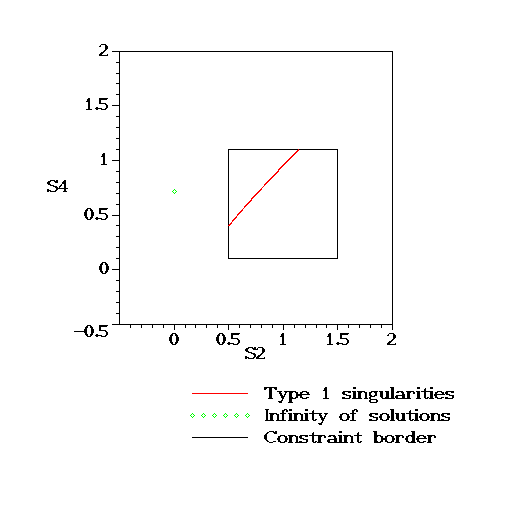
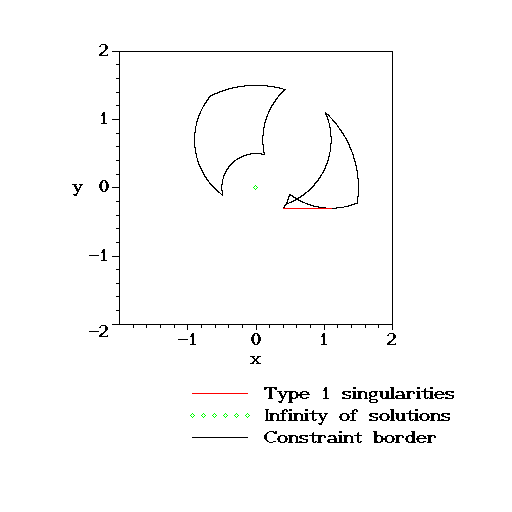
> PlotWorkspace (rprrp, pose);

> PlotWorkspace (rprrp, [S2,x]);

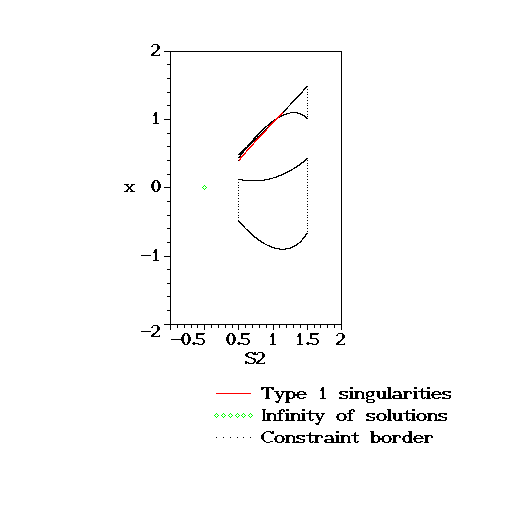
Configurations

Configurations := proc ( robot ::Manipulator,
spec ::seq(name=constant),
{
noconstraints ::truefalse := false,
ordering ::name := NULL
}    )

Computes the different possible positions.

Parameters

robot	an object of type Manipulator
spec	sequence of name=constant: the specification of the known variables (the articular values or the pose values, or other)
noconstraints=b (optional)	b is a boolean: when true, the constraint inequalities are ignored; default value: false.
ordering (optional)	ordering is a name used to order the solutions; default value: NULL

Returns

A list of elements: each elements is a list of name=list(constant) and represents a configuration of the input manipulator.

Example

> rpr := Parallel_3RPR ():
> Configurations (rpr, r1=20, r2=20, r3=20);
[[A1 = [0., 0.], A2 = [15.91, 0.], A3 = [0., 10.00],

    B1 = [1.238874219, -19.96159289], B2 = [18.27856689, -19.85925202],

    B3 = [14.37838350, -3.78571901]], [A1 = [0., 0.], A2 = [15.91, 0.],

    A3 = [0., 10.00], B1 = [-15.37568723, 12.79016193],

    B2 = [1.62170358, 13.99444837], B3 = [-3.30997940, 29.78205101]], [

    A1 = [0., 0.], A2 = [15.91, 0.], A3 = [0., 10.00],

    B1 = [19.99999727, -0.01045036340], B2 = [31.39060352, 12.66297417],

    B3 = [16.87622894, 20.59410427]], [A1 = [0., 0.], A2 = [15.91, 0.],

    A3 = [0., 10.00], B1 = [-13.64842837, -14.61917929],

    B2 = [-4.083315519, -0.51704413], B3 = [-19.53983068, 5.37074264]]]

PlotRobot2D

PlotRobot2D := proc (
    robot ::Manipulator,
    spec ::seq(name=constant),
    k ::{integer,range,list(integer)} := ..,
    {
    color := [],
    legendvars := subs (map(s->lhs(s)=NULL,[spec]), [op(robot:-ArticularVariables), op(robot:-PoseVariables), op(robot:-PassiveVariables), 'det(J)']),
    nolegend ::truefalse := false,
    noconstraints ::truefalse := false
    }
)

Plot a planar manipulator

Parameters

robot	a Manipulator: the robot to plot
spec	a sequence of name=constant: specification of variables of the robot to plot
k (optional)	an integer: specifies one of the possible configuration when several are available
color=col (optional)	equation of the shape color=col, where col is a color or a list of colors; when the number of specified color is not enough, deterministic colors are chosen; default value: empty list.
legendvars (optional)	list of names: the variables to display in the legend; default value: the articular, passive and pose variables, minus the variables in spec
nolegend=b (optional)	b is a boolean: when false, a legend is displayed (the graphic appears in a separate windows with a classic worksheet); default value: false.

Returns

A graphic: the different configurations of the manipulator satisfying the input specifications. (Maple 13 and higher only)

Example

> rpr := Parallel_3RPR ():
> PlotRobot2D (rpr, r1=20, r2=20, r3=20);

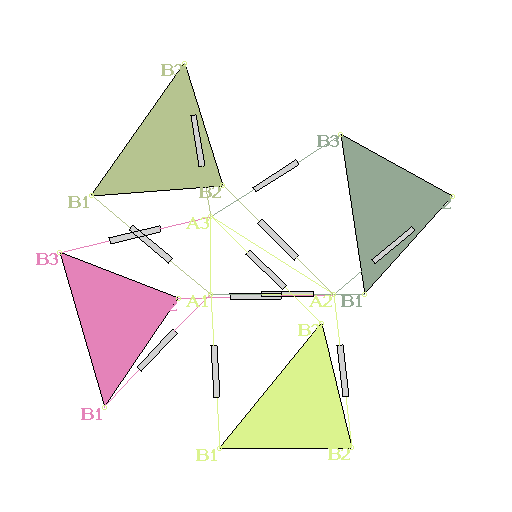
> rr := Parallel_2RR():
> plots:-animate (PlotRobot2D, [rr, theta1=1+t, theta3=2-t], t=0..1);

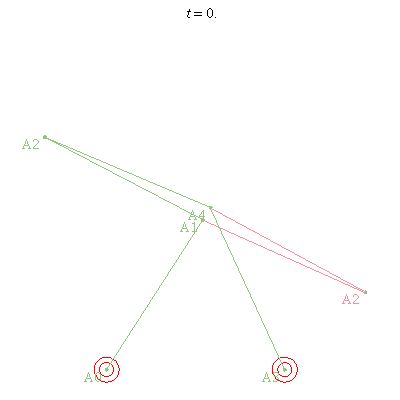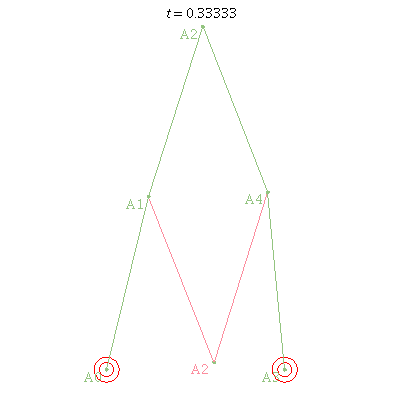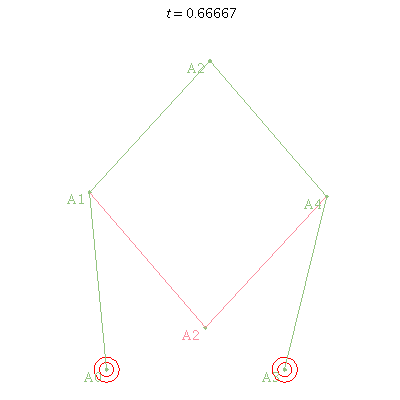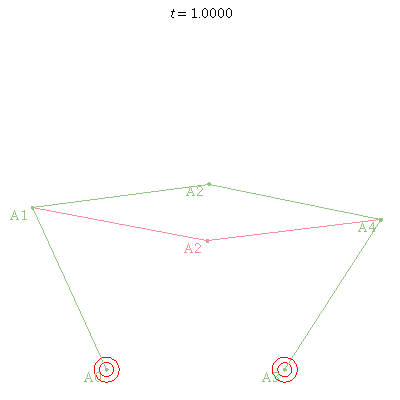
PlotRobot3D

PlotRobot3D := proc (
    robot ::Manipulator,
    spec ::seq(name=constant),
    k ::{integer,range,list(integer)} := ..,
    {
    color := [],
    legendvars := subs (map(s->lhs(s)=NULL,[spec]), [op(robot:-ArticularVariables), op(robot:-PoseVariables), op(robot:-PassiveVariables), 'det(J)']),
    nolegend ::truefalse := false,
    noconstraints ::truefalse := false,
    nolabel ::truefalse := false
    }
)

Plot a 3D manipulator

Parameters

robot	a Manipulator: the 3D robot to plot
spec	a sequence of name=constant: specification of variables of the robot to plot
k (optional)	an integer: specifies one of the possible configuration when several are available
color=col (optional)	equation of the shape color=col, where col is a color or a list of colors; when the number of specified color is not enough, deterministic colors are chosen; default value: empty list.
legendvars=l (optional)	l is list of names: the variables to display in the legend; default value: the articular, passive and pose variables, minus the variables in spec
nolegend=b (optional)	b is a boolean: when false, a legend is displayed (the graphic appears in a separate windows with a classic worksheet); default value: false.
nolabel=b (optional)	b is a boolean: when true, no label appears on the articulations; default value: false.

Returns

A graphic: the different configurations of the manipulator satisfying the input specifications. (Maple 13 and higher only)

Example

> robot := Orthoglide():
> PlotRobot3D (robot, r1=1,r2=1,r3=1, 2);

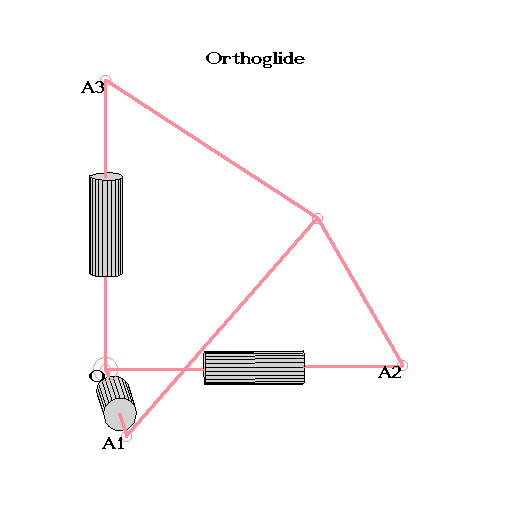
PlotCell3D

PlotCell3D := proc ( cells ::record,
i ::{list(integer),integer} := [ $ 1 .. nops(cells:-SamplePoints) ],
ranges ::seq(name=range) := NULL,
{
nowall ::truefalse := false,
grid ::integer := 10,
border ::constant := 0.0000001,
color := [],
noverbose ::truefalse := false,
verboserate ::integer := -10
}
   )

Plot the cells returned CellDecomposition or CellDecompositionPlus

Parameters

cells	an object returned by CellDecomposition or CellDecompositionPlus
i (optional)	an integer or a list of integer: the indices of the cells to plot in cells. default value: all the cells
ranges (optional)	a sequence of the form v=n1..n2 where v is a variable and n1,n2 are numerical values; when not specified for a variable, the default range is -5..5.
grid = i (optional)	i is an integer leading to a grid size i x i; default value: 10.
border = e (optional)	e is a numeric value: defines the precision on the border; default value: 0.0000001.
nowall = b (optional)	b is a boolean; when b is true the vertical faces are not displayed
color = col (optional)	equation of the shape color=col, where col is a color or a list of colors; when the number of specified color is not enough, deterministic colors are chosen; default value: empty list.
noverbose = b (optional)	b is a boolean: if true, no verbose is displayed; default value: false
verboserate = i (optional)	i is an integer: if positive (resp. negative) the number (resp. the pourcentage) of cells computed before displaying a new verbose line; default value: -10 Returns: A 3D plot of the cells indiced by i in cells.

Example

> cells := CellDecompositionPlus ([T],[25-(x^2+y^2+z^2),x+y],[T],[x,y,z]):
> PlotCell3D (cells,[11,15],color=blue);

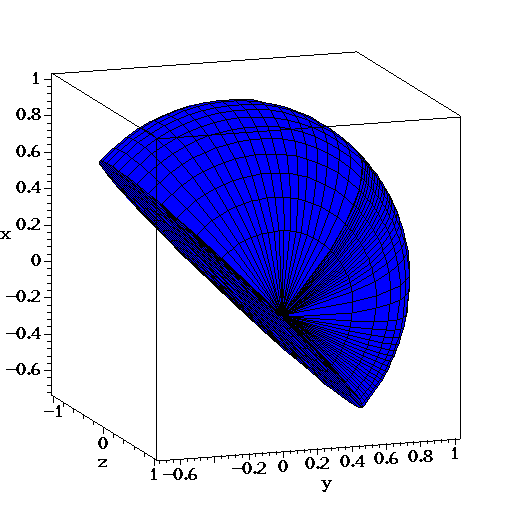
PlotCell2D

PlotCell2D := proc (
    cells ::record,
    i ::{list(list(integer)),list(integer),integer} := [ $ 1 .. nops(cells:-SamplePoints) ],
    ranges ::seq(name=range) := NULL,
    {
    samplepoints ::truefalse := false,
    nowall ::truefalse := false,
    grid ::integer := 10,
    border ::constant := 0.0000001,
    color := [],
    downupcolors ::list := [],
    points ::list := [],
    colorpoints ::list := [],
    noverbose ::truefalse := false,
    verboserate ::integer := -10
    }

)

Plot the cells returned CellDecomposition or CellDecompositionPlus

Parameters

cells	an object returned by CellDecomposition or CellDecompositionPlus
i (optional)	an integer, a list of integer or a list of list of integer: the indices of the cells to plot in cells. default value: all the cells
ranges (optional)	a sequence of the form v=n1..n2 where v is a variable and n1,n2 are numerical values; when not specified for a variable, the default range is -5..5.
grid = i (optional)	i is an integer leading to a grid size i x i; default value: 10.
border = e (optional)	e is a numeric value: defines the precision on the border; default value: 0.0000001.
nowall = b (optional)	b is a boolean: when b is true the vertical faces are not displayed; default value: false.
color = col (optional)	equation of the shape color=col, where col is a color or a list of colors; when the number of specified color is not enough, deterministic different colors are chosen; default value: empty list.
samplepoints = b (optional)	b is a boolean; if true, the labels of the cells are displayed; default value: false.
downupcolors = ducol (optional)	list stating the colors of the lower and upper borders of each cell in the follwing form: [[downcol_cell1, upcol_cell1], [downcol_cell2, upcol_cell2],...] default value: empty list.
points = pts (optional)	list of coordinates of points to be plot of the form [[x1,y1], [x2,y2], ...] default value: empty list.
colorpoints = colpts (optional)	list of colors for the points specified in “points=pts” of the form [col_pt1, col_pt2, ...] default value: empty list.
noverbose = b (optional)	b is a boolean: if true, no verbose is displayed; default value: false
verboserate = i (optional)	i is an integer: if positive (resp. negative) the number (resp. the pourcentage) of cells computed before displaying a new verbose line; default value: -10

Returns

A 2D plot of the cells indiced by i in cells.

Example

> cells := CellDecompositionPlus ([T],[25-(x^2+y^2),x+y],[T],[x,y]):
> PlotCell2D (cells,samplepoints);

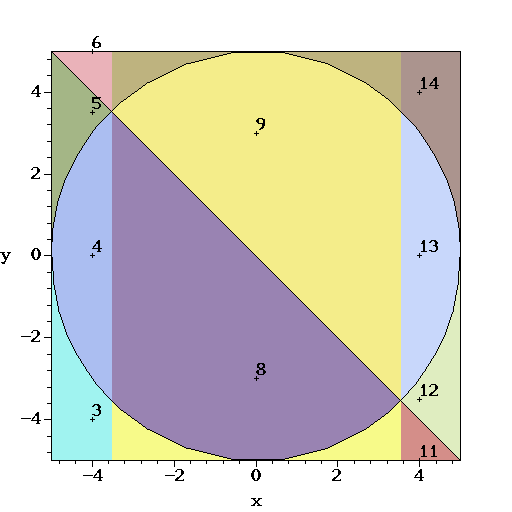
SetCellColors

SetCellColors := proc ( Lc,
Lp )

Set colors to the numbers of solutions obtained by NumberOfSolutionsPlus

Parameters

Lc	list returned by NumberOfSolutionsPlus
Lp	list returned by DVNumberOfSolutionsPlus

Returns

a list of lists C ready to be used by PlotCell2D: C[1] - contains the numbers of the cells to be plotted C[2] - contains the inner colors for the cells C[3] - contains the colors for the lower and upper borders of the cells C[4] - contains the coordinates of the points to be plotted C[5] - contains the colors for the points to be plotted.

Path

Path := proc ( L ::list,
steps ::integer := 10 )

Interpolate points linearly.

Parameters

L	list of points.
steps	integer: the number of interpolated points.

Returns

A list of list of steps points; the linear interpolation between the input points of L.

Trajectory

Trajectory := proc ( L ::list,
steps ::integer := 20,
{
color := []
}
   )

Display a given trajectory.

Parameters

L	list or list of list of points in the plane or 3d space.
steps	integer: the number of interpolated points.
color (optional)	a color name or a list of color names; default value: [].

Returns

A plot of the given trajectory:

if the input is a list of list of points, then the i-th list is a path colorized with the i-th element of color (or with color directly if it is a color name). If there is no i-th color, a random color is chosen.
if the input is a list of points, then a list of list of points is created by computing steps points between 2 consecutive points. Then this list of list is displayed.

Example

> Trajectory ( [[0,0],[1,1],[-1,1]],     # the list of vertices
               color=[blue,red] );       # colors of the edges

ImageTrajectory

ImageTrajectory := proc ( robot ::Manipulator,
L ::list,
pars ::list(name) := robot:-ArticularVariables,
vars ::list(name) := robot:-PoseVariables,
steps ::integer := 20,
{
color := [],
loop ::truefalse := false
}
   )

Display a given trajectory.

Parameters

robot	the manipulator under study
L	list or list of list of points; a point is a list of numerical values, coordinates of the variables pars;
pars	list of name; default value: robot[ArticularVariables].
vars	list of name: the image space, a list of 2 or 3 variables; default value: robot[PoseVariables].
steps	integer: the number of interpolated points.
color (optional)	a color name or a list of color names; default value: [].
loop (optional)	a boolean: if true and L is a list of vertices, then the last point is connected to the first one.

Returns

A plot of the given trajectory:

if the input is a list of list of points, then the i-th list is a path colorized with the i-th element of color (or with color directly if it is a color name). If there is no i-th color, a random color is chosen.
if the input is a list of points, then a list of list of points is created by computing steps points between 2 consecutive points. Then this list of list is displayed.

Example

> robot := ParallelRPR2PRR();
> ImageTrajectory (robot,                       # the manipulator
                   [[0,0,0],[1,1,1],[-1,1,1]],  # the list of vertices
                   [S1,alpha2,alpha3],          # the input variables
                   [phi,x, y],                  # the output variables
                   50,                          # number of inbetween points
                   color=[blue,red],            # colors of the edges
                   symbol=soliddiamond);        # additional plot options